
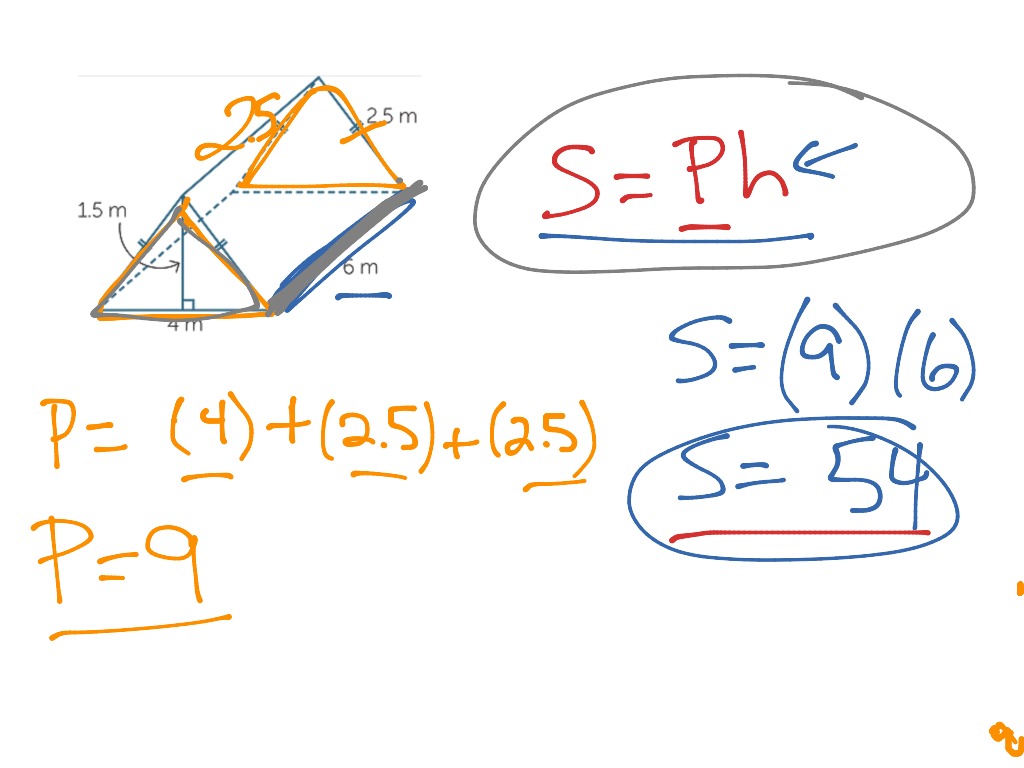
In the end we have also discussed the practical problem based on these topics for better understanding.

We have also come to know about the concept of base area and perimeter of prism. In this post, we have talked about the concept of the surface of a prism and came to know that the surface area of the prism is the total sum of the total space filled by the flat surfaces of the prism. In general, the lateral surface area of a prism is equal to the product of the length of the prism and the perimeter of its base. Therefore the total number of surfaces for a prism with an n sided polygonal base is $n + 2$.Ĭonsider such a prism whose length is $h$ and whose side length and apothem of its base are respectively $b$ and $a$.
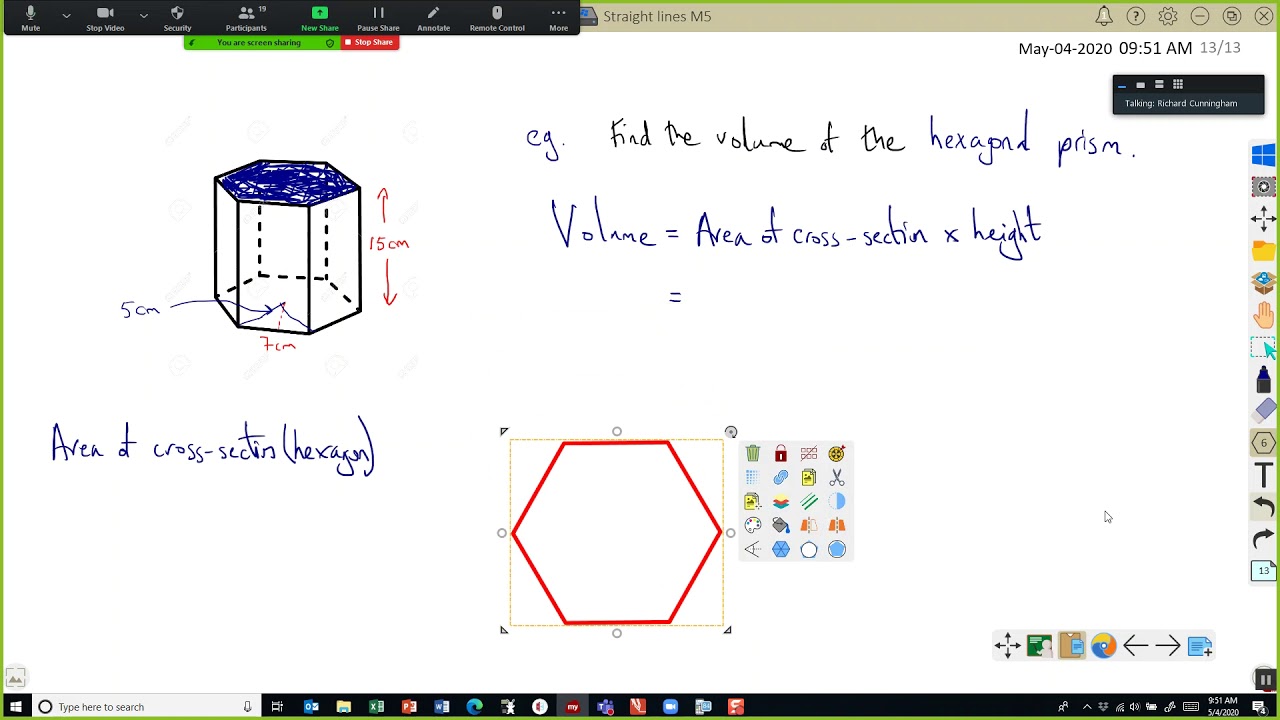
For an $n$ sided base polygon, the prism will have $n$ rectangular faces. The number of lateral surfaces is equal to the number of sides of the base polygon. Surface Area of a Prism Formula - Derivation & Solved ExamplesĪ prism is a polyhedron that has two congruent parallel bases joined by parallelogram or rectangular (in the case of right prisms) faces laterally. Calculating the entire space occupied by all the faces of that particular type of prism, or the sum of the areas of all faces (or surfaces) on a 3D plane, is how you find the surface area of a prism. The amount of total space filled by the flat faces of a prism is referred to as its surface area of a prism. In this article, we are going to discuss the surface area of different types of prisms and various problems based on them. A prism's surface area is the entire area filled by the prism's faces. A three dimensional solid prism's surface area is determined by the form of its base.


 0 kommentar(er)
0 kommentar(er)
